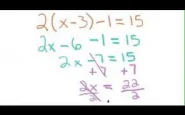I logaritmi sono strumenti utili per la risoluzione di equazioni in cui è incluso x come esponente. Un esponente indica quante volte un numero viene moltiplicato per se stesso in una equazione. Se avete l’equazione 2^x = 90, o 2 alla potenza x = 90, è possibile semplificare l’equazione prendendo il logaritmo naturale di entrambi i lati. Finché si è sicuri di prendere il logaritmo naturale di entrambi i lati, i risultati saranno equivalenti all’equazione originale.
istruzioni
1. Prendere il logaritmo naturale delle quantità di ogni lato dell’equazione. Se si sta lavorando con l’equazione 3^(x + 7) = 17, riscrivere l’equazione come ln (3 ^ (x + 7)) = ln (17).
2. Riscrivere la metà sinistra dell’equazione. Utilizzare l’identità che ln (a ^ x) è uguale a x ln (a), per riscrivere la metà sinistra (x + 7) * ln (3) = ln (17).
3. Isolare il LNS (logaritmi naturali) su un lato dell’equazione dividendo entrambi i lati dell’equazione da ln (3). Otterrete la nuova identità, x + 7 = ln (17) / ln (3).
4. Utilizzare una calcolatrice per interpretare il lato sinistro dell’equazione. Otterrete x + 7 = 2,578.
5. Sottrarre 7 da entrambi i lati dell’equazione, per ottenere x = -4,42.