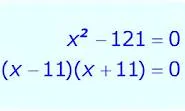Come fattorizzare un'espressione quadratica

Un’espressione quadratica è un polinomio con la struttura di “ax ^ 2 + bx + c”. La “x” si riferisce all’incognita, mentre “a”, “b” e “c” sono i coefficienti. La soluzione fattorizzata sarà in forma di (x + d) (x + e). Il trucco è quello di aggiungere “d” ed “e” a “b” mentre contemporaneamente si moltiplicano per “c”.

istruzioni

1. Annotare (x +) (x +) per iniziare la soluzione. Assicurarsi di lasciare spazio per i numeri prima di “x” e dopo i segni più.

2. Scrivete tutte le coppie di numeri che si moltiplicano insieme per eguagliare l’ultimo numero dell’equazione di secondo grado. Ad esempio, se l’equazione è x ^ 2 + 7x + 10, le coppie disponibili sono (10,1), (5,2), (-10, -1) e (-5, -2), in quanto queste sono solo le coppie di numeri che saranno ugualei a 10, se moltiplicate tra loro.

3. Analizzare le coppie che avete scritto e scegliere quella che è uguale al numero centrale dell’equazione quadratica. Utilizzando l’esempio precedente, la coppia corretta è (5,2) in quanto questi due numeri si sommano in 7 pari al numero centrale.

4. Annotare la coppia che si è determinata come corretta. Nel nostro esempio, che sarebbe (x + 5) (x + 2). L’equazione quadratica è scomposta.