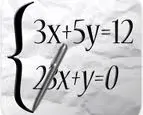La soluzione di una sola equazione contente due variabili può essere trovata graficamente.
Ma, quando si hanno più equazioni con due incognite, si ottiene un sistema di equazioni, le quali possono essere risolte insieme.
Tale sistema può essere risolto con un metodo di sostituzione, il quale sfrutta passaggi algebrici per porre y uguale ad un’equazione e poi usa quanto trovato per risolvere in x nella seconda equazione. Utilizzando lo stesso all’inversa, possiamo trovare il valore di y e così il sistema è interamente risolto.
I passaggi:
- Consideriamo il sistema di equazioni 5x + 3y = 25 e 2x + 4y = 12.
- Isoliamo la variabile y nella seconda equazione, sottraendo 2x a entrambi i membri (4y = 12 – 2x) e dividendo per 4, ricavando così: y = 3 – (1/2)x.
- Sostituiamo l’espressione di y appena trovata nella prima equazione: 5x + 3(3 – 1/2x) = 25. Risolviamo il prodotto: 5x + 9 – (3/2)x = 25 e sottraiamo 9 ad ambo i membri: 5x – (3/2)x = 16. Ora, trasformiamo 5 in 10/2, in modo tale da poter operare la somma di frazioni, ottenendo (7/2)x = 16. Moltiplicando per il reciproco di 7/2, cioè 2/7, si ottiene il valore di x, che è x = 32/7.
- Sostituendo la x appena trovata nell’espressione che ci fornisce la y (quella trovata al punto 2), si ottiene y = 3 – 1/2(32/7) = 3 – 32/14 = 3 – 16/7. Ora, come prima, trasformiamo 3 in una frazione, precisamente: 3 = 21/7. In definitiva, si ottiene y = 21/7 – 16/7, cioè y = 5/7.